Phenomenology of hadron physics
Due to its non-perturbative nature in the low-energy regime, the strong interaction poses a unique challenge within the standard model of particle physics. This working group uses theoretical techniques in order to describe or predict experimental data, where this connection is commonly referred to as phenomenology. Some of the most broadly shared topics within this group are briefly presented below; however, this website cannot cover all projects and for a more complete picture we refer to the publications. The GitHub organization of this group can be accessed via the button on the right.
Anomalous magnetic moment of the muon
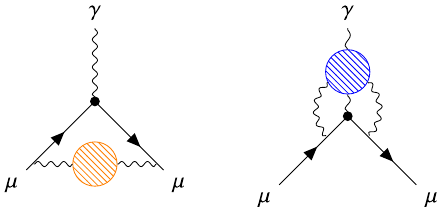
The Dirac equation predicts a lepton's magnetic moment to be proportional to its spin, with the factor of proportionality, the gyromagnetic ratio g, given by g = 2. The anomalous magnetic moment captures the observed deviation aμ=(g - 2)/2. For the muon, the experimental value of aμ deviates from the theoretical estimate presented in the White Paper. The two contributions that have the largest uncertainties in the standard-model calculation come from the hadronic vacuum polarization (left) and the hadronic light-by-light scattering (right) diagrams. In this group, we calculate processes that contribute to these two quantities and can therefore improve the standard-model prediction of the anomalous magnetic moment of the muon.
Final-state interactions
Exact knowledge of final-state interactions is necessary to extract observables to very good precision from experiment. This group uses dispersive techniques, based on the S-matrix principles of unitarity and analyticity, for many applications. The simplest example is the pion vector form factor, where the two-pion rescattering can be treated via the Omnès function. A well-constrained pion vector form factor is important since it serves as an input to many other reactions, e.g., the kaon vector form factor. These quantities are also used in calculations of the anomalous magnetic moment of the muon.
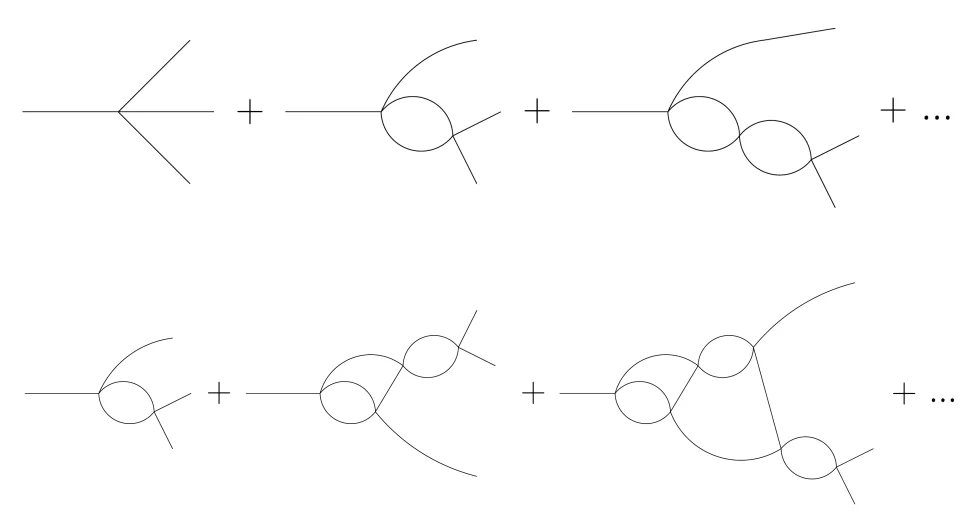
More complicated applications are three-body decays, which are usually treated in isobar-type models. There, one particle is treated as a spectator and it is assumed that only the remaining two particles undergo final-state interaction (top diagram). However, full rescattering effects (bottom diagram) can be calculated via Khuri-Treiman equations, where we published a rather general code for the solution of these integral equations. Furthermore, Khuri-Treiman equations can also be used in low-energy scattering reactions to treat the crossed-channel rescattering effects correctly.
Symmetries and symmetry violation
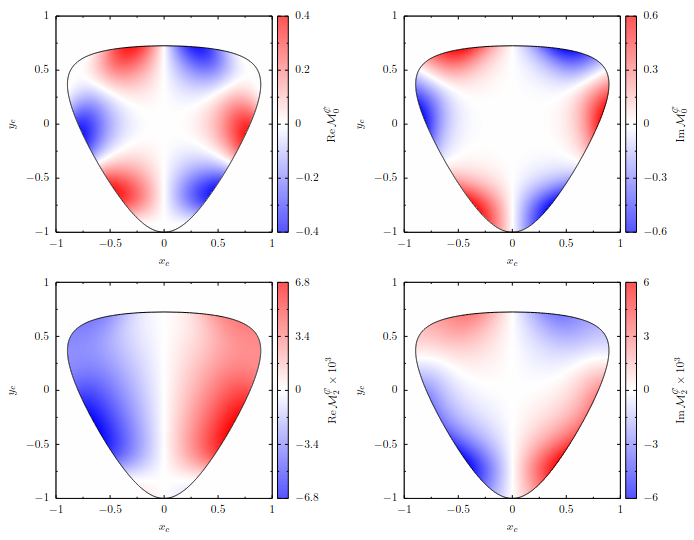
In the standard model, the strong interaction preserves charge conjugation C, parity P, and time-reversal T symmetry individually. However, there is experimental evidence for CP violation beyond the CKM mechanism. Often, CP violation is induced via P violation (e.g., via the QCD θ-term), which is however rigorously constrained by the electric dipole moment of the neutron. Therefore, one can study another source of CP violation via C violation and construct T-odd and P-even (TOPE) operators that preserve the CPT theorem. Daliz-plot asymmetries for the C-violating, isospin-0 and -2, η' → 3π decays are shown on the right. Typically, these asymmetries are out of reach with the current experimental precision.
Furthermore, to precisely study CP violation, a well-constrained strong phase shift is necessary. In the B± → K±π+π- system, the pairwise hadronic final-state interactions for small ππ invariant masses are studied. The accurate knowledge of the ππ system at low energies can be incorporated into the B-decay analysis and allows for a better understanding of these CP asymmetries. Additionally, the rescattering of all three final-state particles might be described using Khuri-Treiman equations, similar to the previous paragraph.
Rare decays
If a decay is rare, there is typically a reason for that, e.g., a symmetry that forbids it, or it occurs at a higher order in some perturbative expansion.
Semileptonic η decays are a good example for this: the η meson is an ideal test case for CP violation since it is a C and P eigenstate. Semileptonic decays via one virtual photon (left diagram) violate C and CP symmetry, while decays via the two-photon intermediate state (right diagram) preserve these symmetries, but are loop suppressed. The one-loop diagram can be calculated and therefore allows one to test CP violation beyond the standard model in this channel experimentally. However, the current experimental limits are far above the calculated branching ratios.
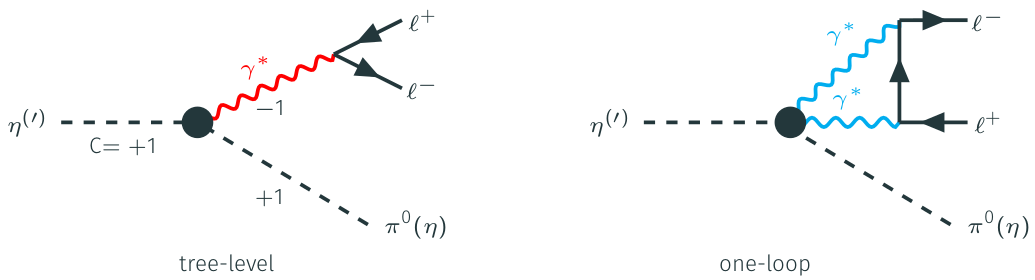
Flavour physics
While the previous examples dealed mostly with the lightest hadrons, their heavier cousins also offer interesting opportunities to test the standard model and its symmetries. Flavour physics refers to the properties and dynamics of hadrons that contain not only the lightest, "unflavoured", but also the heavier charm and bottom quarks. Processes involving, e.g., B and D mesons or exotic hadrons are currently being investigated by experiments, and to learn from the latter, it is important to have good theoretical models at hand. An important class of methods in this field are effective field theories. While the most prominent example, chiral perturbation theory, is constructed for the lightest hadrons, there are different power counting schemes for heavier particles, such as heavy-quark effective theory, heavy-quark spin symmetry, heavy-meson chiral perturbation theory, and non-relativistic effective field theories.